The need for causal inference arises in many different fields. Economists want to quantify the causal effects of interest rate cut on the economy. Trade policy makers want to know whether increased tariff causes changes in trade deficit. Healthcare providers want to assess whether a therapy causes changes in specific patient outcomes. Conceptually, causal inference is all about a question of ‘what if’. People can ask themself what if I took chemotherapy rather than radiation to treat my cancer, would I get better now? Or what if I went to graduate school rather than entering the job market after graduation, would I have a better career prospect? The economists can be curious about what if the Federal Reserve raised the interest rate by 50bp rather than 25bp, would the inflation rate be better controlled? The most straightforward way to answer those questions is, if we know what will happen for any of these actions in advance, we of course can choose the one benefits our goal the most. This leads to the Potential Outcome Framework that we will discuss in the next section.
Potential outcome framework, or Rubin-Neyman potential outcome framework (Donald B. Rubin 1974; Neyman 1923; Imbens and Rubin 2015), is the most canonical framework for causal inference studies. Suppose the treatment has binary levels, denoted as \(T \in \{1,-1\}\), and the corresponding potential outcomes are \(Y^{(1)}\) and \(Y^{(-1)}\), respectively. But people can only observe one realized outcome, i.e., the observed outcome is factual and unobserved outcome is counterfactual. In other words, the outcome can only be either \(Y^{(1)}\) or \(Y^{(-1)}\), which is represented by \[ Y = 1[T = 1]Y^{(1)} + 1[T = -1]Y^{(-1)}. \] The individual causal effect, or individual treatment effect (ITE), is thus defined by \[\begin{equation} \tau_i = Y_i^{(1)} - Y_i^{(-1)} \tag{1} \end{equation}\] for subject \(i\), but it is unobservable in real world.
To make the estimation of causal effect feasible, we have to make several assumptions:
Assumption 1. Stable Unit Treatment Value Assumption (SUTVA) (Donald B. Rubin 1980)
1) Treatment applied to one unit does not affect the outcome for other units (No Interference)
2) There is no hidden variation, for example, different forms or versions of each treatment level, for a single treatment (Consistency)
Assumption 2. Unconfoundedness/Ignorability/Strongly Ignorable Treatment Assignment (SITA) \[\begin{equation} (Y^{(1)}, Y^{(-1)}) \perp T \mid \mathbf X, \label{assump2} \end{equation}\]
Assumption 3. Common Support/Positivity \[\begin{equation} 0 < \Pr(T = 1 | \mathbf X = \mathbf x) =\pi(\mathbf x) < 1 \label{assump3} \end{equation}\] where \(\pi(\mathbf x)\) is called Propensity Score (PS).
In the following sections, we will discuss how to estimate of the individual or sample average treatment effects under this potential outcome framework with these assumptions.
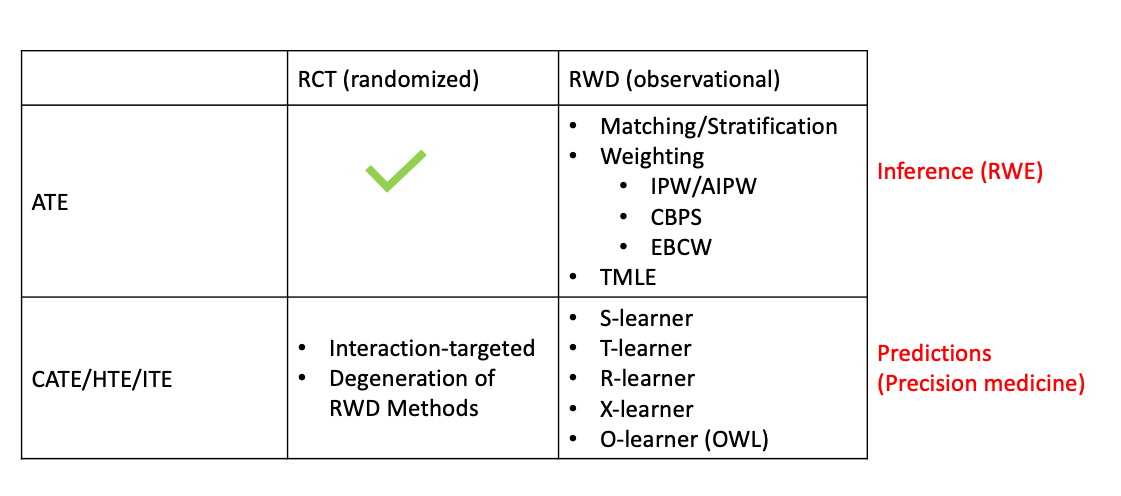
In general, most research on causal inference either studies the population-wise treatment effect, i.e., the average treatment effect (ATE), or the subject-level/individual treatment effect (ITE), i.e., the conditional treatment effect (CATE), which is exchangeable to heterogenuous treatment effect (HTE).
Basically, the observations can be either from randomized experiments, like randomized controlled trial (RCT), or observational studies, so-called real world data (RWD). With different observations, the estimation methods can be very different.
Briefly speaking, the ATE can be easily obtained via well-designed RCTs or A/B tests (we will see why in section Average Treatment Effect). That’s how pharmaceutical/biotech companies evaluate their drug effectiveness. In recent years, a big trend in drug development which is supported by FDA is to use RWD and real world evidence (RWE) to support as well as speed-up the regulatory approval. Since RWD is obervational rather than randomized controlled, a sizable methods are proposed including Matching (Rosenbaum and Rubin 1983; Austin 2014), Subclassification (Rosenbaum and Rubin 1984), Weighting (Hirano, Imbens, and Ridder 2003; Austin 2011; Austin and Stuart 2015), Regression (Donald B. Rubin 1979; D. B. Rubin 1985; Hahn 1998; Gutman and Rubin 2013), or a mixture of them (Bang and Robins 2005; Van Der Laan and Rubin 2006).
Another heat topic in causal inference is about the estimation of CATE/HTE/ITE from observational studies. This is usually tough because given the noise of observational studies and subject-level estimation, the estimates can have large variance. Various of methods have been proposed including but not limited to causal boosting (Powers et al. 2018), causal forests (Athey and Imbens 2016), individual-treatment-rule-based methods that mostly involves outcome weighted learning (OWL) (Qian and Murphy 2011; Zhao et al. 2012; X. Zhou et al. 2017; Qi et al. 2020), and several meta-learners, such as X-learner (Künzel et al. 2019) and R-learner (Nie and Wager 2020). These methods can be easily degenerated to study the CATE/HTE/ITE in randomized trials by replacing the estimated propensity scores to fixed numbers.
Different scientific questions leads to the estimation of different causal estimands. As aforementioned, ATE is basically about assessing the population/sub-population treatment effect which is the key focus for the drug companies. On the other hand, CATE is more about individual-level treatment effect, so it can be used to do precision medicine or personalized recommendations. Here is a list of the acronym of some commonly used causal estimands:
ATE can be observed from well-designed randomized controlled trial (RCT) directly, which reveals the population-wise treatment effect. \[ \begin{aligned} \tau & = E[Y^{(1)} - Y^{(-1)}]\\ & = E[Y^{(1)}] - E[Y^{(-1)}] \quad\text{ (causation)}\\ & = E[Y^{(1)} \mid T = 1] - E[Y^{(-1)} \mid T = -1] \\ & = E[Y \mid T = 1] - E[Y \mid T = -1] \quad\text{ (association)} \end{aligned} \]
The essence here is the randomization eliminates all the confounding effects, or in other words, the Unconfoundedness and Positivity assumptions holds automatically under randomized controlled experiments.
Remark \(E[Y^{(1)}] - E[Y^{(-1)}]\) is the interested causation but is unobservable in real world. By unconfoundedness and positivity, we infer the unobservable causation via observed data, i.e., \(E[Y \mid T = 1] - E[Y \mid T = -1]\), which is also known as association. In general, association does not imply causation.
Another commonly used causal estimand is average treatment effect for the treated (ATT), which focus on the population receive the treatment \[ \tau^{\text{ATT}} = E[Y^{(1)} - Y^{(-1)}\mid T = 1]. \]
Propensity score (PS) (Rosenbaum and Rubin 1983) is defined as the conditional probability of receiving a treatment given pre-treatment covariates \(\mathbf X\). PS is the very core part in doing causal analysis, especially in the observational studies (but even in randomized trials, PS can be used to do some covariates adjustment for better results).
Though Matching is also a very popular approach in ATE estimation, here we discuss Weighting in details.
The very beginning idea of estimating ATE (under the Assumption 1, 2 and 3) by first finding pairs of observations with covariates close enough to each other in two arms, and then average them out: \[ \tau = E_{\mathcal X}\{E[Y|\mathbf X \in \mathcal X_j, T = 1]-E[Y|\mathbf X\in \mathcal X_j, T = -1]\} \] where \(\mathcal X_j\) is a subspace such that \(\bigcup_{j=1}^J \mathcal X_j = \mathcal X\) and \(\mathcal X_i \bigcap \mathcal X_j = \phi\) for any \(i\neq j\). One-to-one paired matching is hard to find, especially when \(\mathcal X\) is of high dimension. So people propose to use subclassification or coarsened, which also provide more robust estimations.
The matching idea is finally ruled by the milestone work from Rosenbaum and Rubin (1983) who demonstrated that only matching by propensity score is good enough, because \[ (Y^{(1)}, Y^{(-1)}) \perp T \mid \mathbf X \Rightarrow (Y^{(1)}, Y^{(-1)}) \perp T \mid \pi(\mathbf X ). \] The whole matching task is transformed from a potential high diemensional covariate space \(\mathcal X\) to a linear scalar. \[ \begin{aligned} & E_{\pi(\mathbf X)}\{E[Y \mid T = 1, \pi(\mathbf X)] - E[Y \mid T = -1, \pi(\mathbf X)] \} \\ =& E_{\pi(\mathbf X)}\{E[Y^{(1)} \mid \pi(\mathbf X)] - E[Y^{(-1)} \mid \pi(\mathbf X)]\} \\ =& E[Y^{(1)} - Y^{(0)}] = \tau \end{aligned} \] But how to achieve a good estimator of propensity score \(\pi(\cdot)\) turns out to be the key problem.
It can be shown that (Proof in Appendix) \[ E[Y^{(t)}] = E\left[\frac{1[T = t]Y}{Pr(T=t \mid \mathbf X)}\right] \] which leads to \[\begin{equation} \tau = E[Y^{(1)} - Y^{(-1)}] = E\left[\frac{1[T = 1]Y}{\pi(\mathbf X)}\right] - E\left[\frac{1[T = -1]Y}{1-\pi(\mathbf X)}\right]. \tag{2} \end{equation}\] Thus, the estimator of ATE based on observed dataset is \[ \hat\tau = \frac{1}{n}\sum_{i:t_i =1} \frac{y_i}{\hat \pi(\mathbf x_i)} - \frac{1}{n}\sum_{i:t_i =-1} \frac{y_i}{1-\hat \pi(\mathbf x_i)}. \] As this approach can be traced back to Horvitz and Thompson (1952), sometimes it is refered to as Horvitz–Thompson (HT) estimator (Imai and Ratkovic 2014). Since directly weighting on the inverse of propensity score may cause large variability when estimated \(\pi(\mathbf x_i)\) is either close to 1 or 0, Hirano, Imbens, and Ridder (2003) propose to standardize the weight by \[ \hat\tau = \sum_{i:t_i =1} \frac{y_i}{\hat \pi(\mathbf x_i)}\Big/\sum_{i:t_i =1}\frac{1}{\hat \pi(\mathbf x_i)} - \sum_{i:t_i =-1} \frac{y_i}{1-\hat \pi(\mathbf x_i)}\Big/\sum_{i:t_i =-1}\frac{1}{1-\hat \pi(\mathbf x_i)}. \] In our simulation studies, to distinguish from HT, IPW is refered to this standardized weighting method. Similarly, for ATT, it can be estimated by \[ \begin{aligned} \tau^{\text{ATT}} =& E[Y^{(1)} - Y^{(-1)}\mid T = 1] = E[Y^{(1)}\mid T=1] - E[Y^{(-1)}\mid T=1]\\ =& \frac{1}{\pi}\left(E[1[T=1]Y^{(1)}]+E[1[T=-1]Y^{(-1)}] - E\left[\frac{1[T = -1]Y}{1-\pi(\mathbf X)}\right]\right) \\ =& \frac{1}{\pi}E\left[\left(1-\frac{1[T = -1]}{1-\pi(\mathbf X)}\right)Y\right] = \frac{1}{\pi}E\left[\left(\frac{1[T = 1]-\pi(\mathbf X)}{1-\pi(\mathbf X)}\right)Y\right] \\ =& \frac{1}{n_1}\left(\sum_{i:t_i=1}y_i - \sum_{i:t_i=-1}\frac{\pi(\mathbf x_i)}{1-\pi(\mathbf x_i)}y_i\right) \quad \text{for finite sample estimation} \end{aligned} \] where the second equation comes from: \[ \begin{aligned} & E\left[\frac{1[T = -1]Y}{1-\pi(\mathbf X)}\right] = E[Y^{(-1)}] = E[Y^{(-1)}\mid T=1]\Pr(T=1) + E[Y^{(-1)}\mid T=-1]\Pr(T=-1)\ \\ \Rightarrow & E[Y^{(-1)}\mid T=1] = \frac{1}{\pi}\left(E\left[\frac{1[T = -1]Y}{1-\pi(\mathbf X)}\right] - E[1[T=-1]Y^{(-1)}]\right) \end{aligned} \]
J. M. Robins, Rotnitzky, and Zhao (1995) augmented the IPW by a weighted average of the outcome model \[\begin{align} \tau^{\text{AIPW}} =& \underbrace{E\left[\frac{1[T = 1]Y}{\pi(\mathbf X)}\right] - E\left[\frac{1[T = -1]Y}{1-\pi(\mathbf X)}\right]}_\text{IPW} \nonumber \\ &- \underbrace{E\left[\frac{1[T=1] -\pi(\mathbf X)}{\pi(\mathbf X)}\mu_1(\mathbf X) + \frac{1[T=1] -\pi(\mathbf X)}{1-\pi(\mathbf X)} \mu_{-1}(\mathbf X)\right]}_\text{Augmentation} \tag{3} \end{align}\] This AIPW is called “doubly robust” because it is consistent as long as either the treatment assignment mechanism or the outcome model is correctly specified (Kurz 2021). If the propensity score is correctly specified, then \(E(1[T=t] - \Pr(T=t\mid \mathbf X)) = E\left[E(1[T=t] - \Pr(T=t\mid \mathbf X)\mid \mathbf X)\right] = 0\) which simplifies AIPW to IPW no matter whether response surface functions \(\mu_T()\) are correct. On the other hand, if response model \(\mu_T()\) are correctly specified but propensity score is not correctly estimated, AIPW reduces to S- or T-learner (definitions are in the next section. Proof in Appendix)
The very nature of weighting is it helps to make sure the confounding covariates distribution between the observed two arms are balanced. If covariate balancing is guaranteed, then the observed data can mimic the randomized trial data and the treatment effect can be directly obtained from observations. Imai and Ratkovic (2014) propose to directly target on the covariate balancing instead of weighting. So they developed a Covariate Balancing Propensity Score (CBPS) method which is a propensity score estimating method that yields the PSs improve the covariate balancing. The core idea of CBPS is fit a logistic PS model–maximize the likelihood function–subject to covariate balancing constraints. Specifically, the logistic PS model looks like \[ \hat\beta = \arg\min_{\beta\in\Theta} \quad -\sum_{i=1}^N T_i\log\pi(\mathbf X_i;\beta)+(1-T_i)\log(1-\pi(\mathbf X_i;\beta)) \] which is equivalent to (take derivative w.r.t. \(\beta\)) \[ E\left[\frac{ T_i \tilde {\mathbf X}_i}{\pi(\mathbf X_i;\beta)} - \frac{ (1-T_i) \tilde {\mathbf X}_i}{1-\pi(\mathbf X_i;\beta)}\right] = 0 \] where \(\tilde {\mathbf X}_i = \pi'(\mathbf X_i;\beta)\) which is the first derivative of \(\pi(\mathbf X_i;\beta)\) over \(\beta\). The balancing conditions are \[ E\left[\frac{T_i f(\mathbf X_i)}{\pi(\mathbf X_i ; \beta)}\right] = E\left[\frac{(1-T_i)f(\mathbf X_i)}{1 - \pi(\mathbf X_i ; \beta)}\right] \] where \(f()\) can be any type of function that intended to be balanced, including first moment \(\mathbf X\), second moment \(\mathbf X^2\), interaction \(\mathbf X_i \mathbf X_j, i\neq j\), etc. When \(f(\mathbf X_i) = \tilde {\mathbf X}_i\), CBPS is exactly the MLE of logistic regression. If \(\tilde {\mathbf X}_i = \mathbf X_i\) (a linear logistic model), the number of constraints is equal to the number of parameters, which is called exact CBPS. But we can manually add more constraints to make sure higher moments of covariates are balanced as well, then we have more constraints than the covariates, which is call over-identified CBPS. But “overidentifying restrictions generally improve asymptotic efficiency but may result in a poor finite sample performance” (Imai and Ratkovic 2014). The caveat of CBPS is, even PS model is completely misspecificed, the imposed moments (of \(X\), \(X_iX_j\)) are still balanced. CBPS largely avoids extremely propensities and thus, is more robust and better balance.
CBPS is just one of the Covariate-Balancing-type method to obtain the weights. There are many other methods following this idea (Hainmueller 2012; Chan, Yam, and Zhang 2016; Pirracchio and Carone 2018; Huling and Mak 2020) but will not be introduced here.
Another estimator that is receiving more attention for ATE estimation is the targeted maximum likelihood estimator (TMLE) (Van Der Laan and Rubin 2006), which also enjoys the double robustness as AIPW along with other desired features like efficient and aysmptotically linear (allows for construction of valid Wald-type confidence intervals). Either \(\hat\mu_i(\cdot)\) and \(\hat\pi(\cdot)\) are correctly specified leads to consistent estimator while if both are consistently estimated, TMLEs achieve the semi-parametric efficiency bound (Van Der Laan and Rubin 2006).
TMLE is a two-stage procedure with the first stage to obtain an initial estimate of response surface/conditional mean response \(\hat\mu_1(\mathbf X)\) and \(\hat\mu_{-1}(\mathbf X)\). If the initial estimator response surfaces is consistent, the TMLE remains consistent; but if the initial estimator is not consistent, the subsequent targeting step provides an opportunity for TMLE to reduce any residual bias in the estimate of the parameter of interest. Specifically, TMLE solves the efficient influence curve estimating equation for the target parameter (ATE here) in the second stage, which fluctuate/correct the initial estimation on the correct direction as a one-step estimator. The whole idea is supported by the semiparametric theory and here are some references: Semiparametric theory; Nonparametric efficiency theory in causal inference; influence functions.
\[ \hat\tau^{\text{TMLE}}(\mathbf X) = \hat\mu_1(\mathbf X) - \hat\mu_{-1}(\mathbf X) + \hat\varepsilon \left(\frac{1[T=1]}{\hat\pi(\mathbf X)} - \frac{1[T=-1]}{1-\hat\pi(\mathbf X)}\right) \] where \(\varepsilon\) is a flunctuation parameter to update the initial estimation of response surfaces \(\hat\mu_1(\mathbf X) - \hat\mu_{-1}(\mathbf X)\) using the information from propensity score, just like other doubly-robust estimator or X-learner. \(\varepsilon\) can be estimated by fitting ‘clever covariate’ \(H(T, \mathbf X) = \frac{1[T=1]}{\hat\pi(\mathbf X)} - \frac{1[T=-1]}{1-\hat\pi(\mathbf X)}\) on the residual \(Y - \mathbb E[Y\mid T, \mathbf X] \sim H(T, \mathbf X)\).
After introducing this much methods, we would like to provide a high-level picture of how and when to use these methods. Usually, there are two-step included in propensity score (PS) related methods in causal estimand estimation.
The first step is to estimate the propensity score. There are several commonly adopted branches:
In second step, we plug in the propensity score estimated from the first step for the desired estimand. The common approaches for ATE/ATT include:
Sometimes also known as Heterogeneous Treatment effect (HTE). With assumption 1, 2, and 3, it’s definition under two-arm scenario is \[ \begin{aligned} \tau(\mathbf x) &= E[Y^{(1)} - Y^{(-1)} \mid \mathbf X = \mathbf x] \\ &=E(Y \mid \mathbf X = \mathbf x, T = 1) - E(Y \mid \mathbf X = \mathbf x, T = -1) \end{aligned} \]
As discussed, the CATE estimation under randomized setting is generally a special case of those methods under observational studies. Nonetheless, we want to briefly introduce some interaction-oriented methods that are more suitable in randomized setting.
Without loss of generality, outcome \(Y\) can be written by \[ E(Y) = f(\mathbf X) + 1[T=1]g(\mathbf X), \] then \(E(Y\mid \mathbf X = \mathbf x, T = 1) = f(\mathbf x)+g(\mathbf x)\), \(E(Y\mid \mathbf X = \mathbf x, T = -1) = f(\mathbf x)\), and therefore, \(\tau(\mathbf x) = g(\mathbf x)\). So the problem of estimating treatment effect, or subgroup identification turns to be figuring out \(g(\mathbf x)\). Notice that here \(1(T=1)\) is independent of covariates \(\mathbf X\), reflecting the nature of randomized trial.
Also be aware that the covariates of \(f(\cdot)\) and \(g(\cdot)\) could be different. Denote \(\mathcal Z\) and \(\mathcal V\) are two subspaces of origincal covariate space \(\mathcal X\), and \[ E(Y) = f(\mathbf V) + 1[T=1]g(\mathbf Z), \] where \(\mathbf Z \in \mathcal Z, \mathbf V \in \mathcal V\), and \(\mathcal V\) and \(\mathcal Z\) can have overlap. Generally, covariates in \(\mathbf V\) are called diagnostic variables and \(\mathbf Z\) are predictive variables (Imai, Ratkovic, et al. 2013). Some variables are predictive only, indicating that they only react to the treatment; some variables are diagnostic only, meaning that they do nothing with treatment but impact the outcome; some variables are both predictive and diagnostic, while some variables play no effect at all. See Figure (1) for illustration.
A bunch of methods are developed following this idea: Interaction trees (Su et al. 2008, 2009), GUIDE (Generalized unbiased interaction detection and estimation) (Loh 2002; Loh, He, and Man 2015), MOB (Model-Based Recursive Partitioning) (Zeileis, Hothorn, and Hornik 2008; Seibold, Zeileis, and Hothorn 2016).
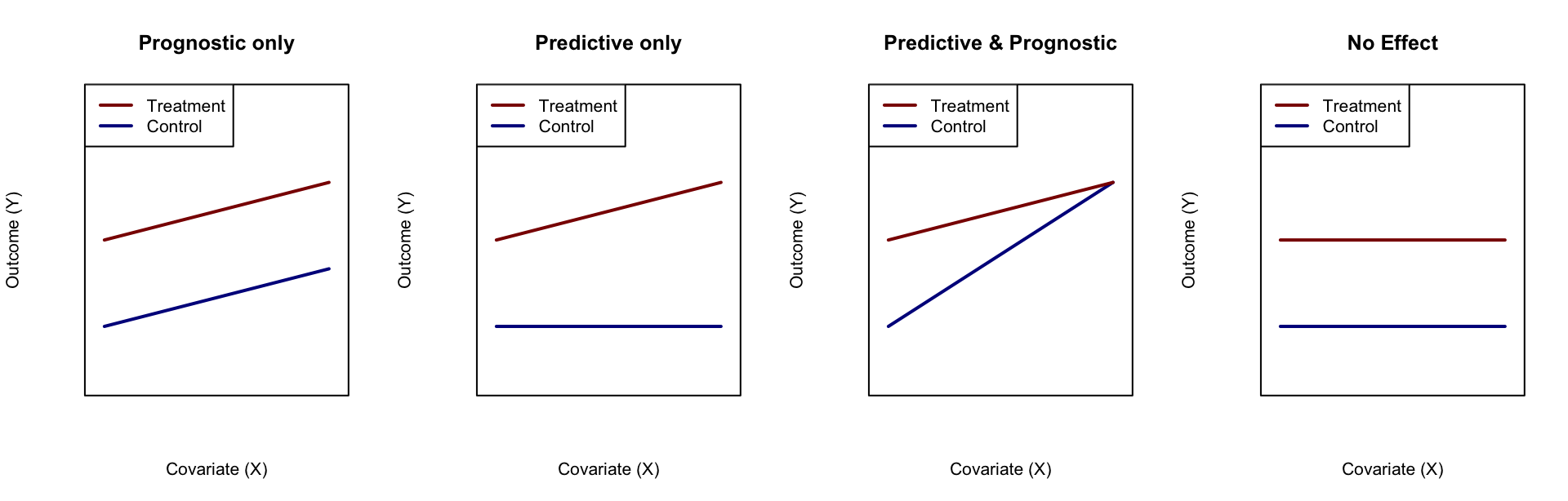
Figure 1: Illustration of predictive and diagnostic variable
Q-learning gets its name because its objective function plays a role similar to that of the Q or reward function in reinforcement learnin (Li, Wang, and Tu 2021) and is first used in estimating optimal dynamic treatment regime (Murphy 2003; J. M. Robins 2004; Schulte et al. 2014). The basic idea is focusing on the estimation of response surfaces \(E[Y \mid \mathbf X, T]\), which is also known as g-computation (J. Robins 1986). So this approach is also called the parametric g-formula (Hernán and Robins 2010) in the literature.
Estimate a joint function \(\hat\mu(\mathbf X, T) = E[Y \mid \mathbf X, T]\) then \[\begin{equation} \hat\tau(\mathbf X) = \hat\mu(\mathbf X, 1) - \hat\mu(\mathbf X, -1). \tag{4} \end{equation}\] This approach is usually named as G-computation estimators, Parametric G-formula, or S-learner. But \(T\) can be neglected or underweighted if \(X\) has high dimension
Estimate response surfaces \(E[Y \mid \mathbf X, T]\) separately, i.e., one function \(\mu_1(\mathbf X) = E[Y \mid \mathbf X, T= 1]\) for \(T=1\) and another \(\mu_{-1}(\mathbf X) = E[Y \mid \mathbf X, T= -1]\) for \(T=-1\). Then \[\begin{equation} \hat\tau(\mathbf X) = \hat\mu_1(\mathbf X) - \hat\mu_{-1}(\mathbf X) \tag{5} \end{equation}\] It is called T-learner. But lose data efficiency as only part of data is used in each model.
The basic idea of advantage-learning or A-learning, is to estimate treatment effect \(\tau(\mathbf x)\) directly, rather than estimating the reponse surfaces like Q-learning which can be deemed as an indirect way. Here are some selected approaches in this camp.
For a 50:50 randomized trial, we can make following transformation (Signorovitch 2007) \[ Y^* = \begin{cases} 2Y \quad &\text{if }\ T=1 \\ -2Y \quad &\text{if }\ T=-1 \end{cases}, \] or equivalently, \(Y^* = 2TY\), and then, we may notice that \[ \begin{aligned} E(Y^*\mid \mathbf X) & = E(Y^*\mid \mathbf X, T = 1)\Pr(T=1) + E(Y^*\mid \mathbf X, T = -1)\Pr(T=-1) \\ & = E(2Y\mid \mathbf X, T = 1)/2 + E(-2Y\mid \mathbf X, T = -1)/2 \\ & = E(Y\mid \mathbf X, T = 1) - E(Y\mid \mathbf X, T = -1) \\ & = \tau(\mathbf X). \end{aligned} \] This means that we can directly fit a model on \(Y^*\) using \(\mathbf X\) and it will return an unbiased estimator of treatment effect (even though the variance could be very large). Similarly, from equation (2), we know that \[\begin{equation} \tau(\mathbf x) = E\left[ \frac{TY}{T\pi(\mathbf X) + (1-T)/2} \;\middle|\; \mathbf X = \mathbf x \right] \tag{6} \end{equation}\] The corresponding transformation or modification of outcome is \(Y^* = \frac{TY}{T\pi(\mathbf X) + (1-T)/2}\) and this MOM-IPW loss function is \[\begin{equation} E[l(\hat\tau, \tau)] = E\left[ \left\{ \hat\tau(\mathbf X)- \frac{TY}{T\pi(\mathbf X) + (1-T)/2} \right\}^2 \right] \tag{7} \end{equation}\]
Notably, this method though simple and straightforward, suffers from the limitation of outcome type and the larger variance.
Observing that we only need to optimize the loss function such as (7), Tian et al. (2014) modified MOM methods by adjusting the proxy loss function a little bit \[ E[\{\hat\tau(X) - Y^*\}^2] = E[c^2\{\hat\tau(X)/c - Y\}^2] \] and then minimizing the right-hand-size, which is the loss function for MCM, targeting on \(\hat\tau(X)\) directly as well. For example, the MCM version of the loss function for randomized trial is thus \[ E\left[ \{\hat\tau(X)\cdot W/2-Y \}^2 \right]. \] For MOM-IPW version, with some modification on (7), the loss function for MCM-IPW version is derived as \[ E\left[ \left\{ \hat\tau(X) \cdot [(W+1)/2 - \pi(X)]- Y \right\}^2 \right] \] and with further adjustment, it turns out to be \[ E\left[ \frac{\left\{ \hat\tau(X)\cdot W- Y \right\}^2}{W\pi(X) + (1-W)/2} \right]. \] So, we no longer need to worry about the outcome type.
R-learner (Nie and Wager 2020) can be considered as a very special case of MCM, but it does not follow the same logic flow as MCM. It adopts the Robinson’s decomposition (Robinson 1988) to connect the CATE with the observed outcome \[\begin{equation} E[Y\mid \mathbf X, T] = m(\mathbf X) + (1[T = 1]- \pi(\mathbf X))\tau(\mathbf X) \tag{8} \end{equation}\] where \(m(\mathbf X) = E[Y \mid \mathbf X]\). In (J. Zhou, Zhang, and Tu), they extended R-learner to multi-armed settings without recommendation inconsistency issue that naturally embedded in most approaches under A-learning framework.
X-learner (Künzel et al. 2019) enjoys the simplicity of T-learner but fixes its data efficiency issue by targeting on the treatment effects rather than the response surfaces. The main procedure is the following:
Notably, when calculating \(\hat\tau_1(\cdot)\), for example, X-learner uses whole data, including instances from both \(T=1\) and \(T=-1\), which is deems as fixing the data efficiency issue in T-learner approach.
Most of the previous methods target on CATE estimation, then the optimal treatment can be found automatically by looking at the estimates. Whereas, obtaining the consistent and unbiased estimates for CATE is difficult in practice. However, if we only need to know which treatment is the optimal, we actually do not need to estimate the CATE but only the treatment assignment rule, or so-called individual-treatment-rule (ITR), \(d(\mathbf x) = sgn\{\tau(\mathbf x)\}\), which is a mapping \(d: \mathcal X \rightarrow T\). In practice, we do not need to estimate \(\tau(\cdot)\) but \(d(\cdot)\) directly. See Figure (2) for a demonstration of the difference between Q-learning, A-learning, and ITR.
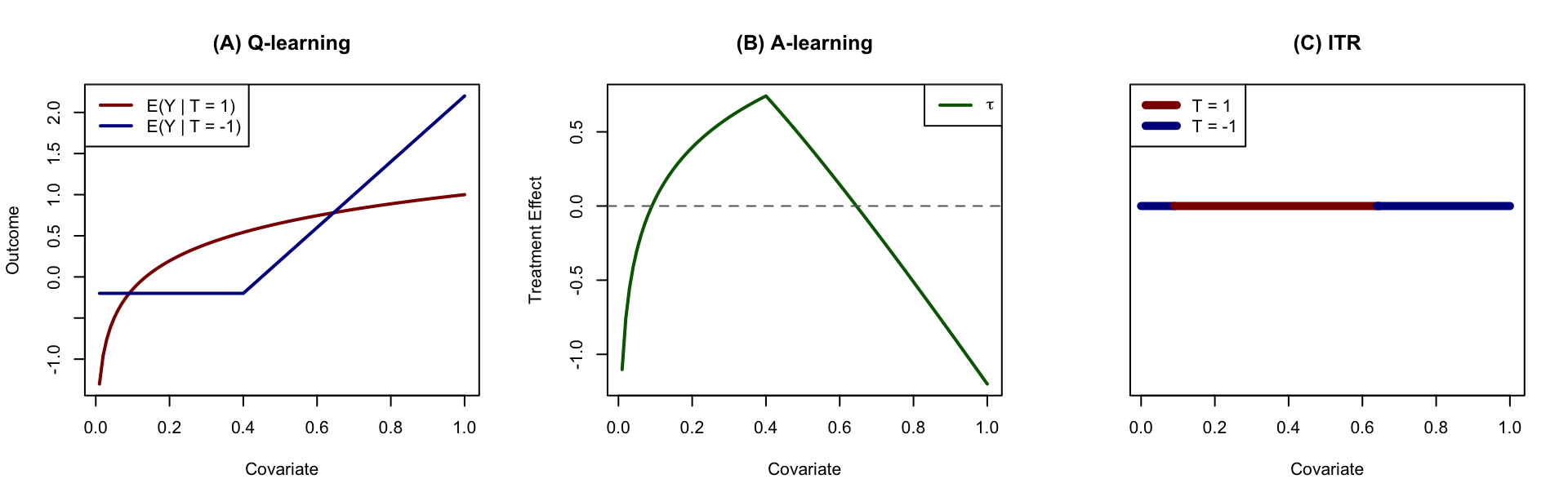
Figure 2: Illustration of causal inference approaches. (A) Q-learning aims at estimating the response surfaces of each treatment group; (B) A-learning aims at estimation of treatment effect directly; (C) ITR aims at estimation of treatment region rather than the treatment effect.
Recall the ITR is indeed a mapping from the covariate space into the treatment space \(d: \mathcal X \rightarrow T\). According to Qian and Murphy (2011) and Zhao et al. (2012), the value function under the ITR \(d(\mathbf X)\) is \[ V(d) =\mathbb E[Y\mid d(\mathbf X)=t] = \mathbb E\left[\frac{1[T = d(\mathbf X)]Y}{\pi(\mathbf X\mid T = t)}\right] \] and the optimal ITR is the one corresponds to the largest value function \[ d^{*}() = \arg\max_{d()} V(d). \] Notice that solving this objective function requires discontinuous loss functions, which may incur certain numerical difficulty. So far, various methods have been proposed in the literature to obtain the ITR following this idea (Qian and Murphy 2011; Zhao et al. 2012; Xu et al. 2015; Zhu et al. 2017; X. Zhou et al. 2017; Zhang and Zhang 2018; Qi et al. 2020). Due to its structure similar to propensity score weighting but only on outcome \(Y\), it is also known as outcome weighted learning, or O-learning (Zhao et al. 2012).
There are many tree-based methods such as virtual trees (Foster 2013), causal tree/forest (Athey and Imbens 2016; Wager and Athey 2018), causal boosting/PTO forest/causal MARS (Powers et al. 2018). Actually, most of them can be categorized as S- or T-learners on a high-level.
(For more details on CATE/HTE estimation, please refer to another post Meta-Learners)
\[ \begin{aligned} & E\left[\frac{1[T = t]Y}{\Pr(T=t \mid \mathbf X)}\right] \\ =& E\left[ E\left(\frac{1[T = t]Y}{\Pr(T=t \mid \mathbf X)} \mid \mathbf X\right)\right] \\ =& E\left[ \frac{E\left(1[T = t]\sum_c1[T=c]Y^{(c)} \mid \mathbf X \right)}{\Pr(T=t \mid \mathbf X)} \right] \\ =& E\left[ \frac{\sum_a E\left(1[T = t]\sum_c1[T=c]Y^{(c)} \mid T = a, \mathbf X \right)\Pr(T = a\mid \mathbf X)}{\Pr(T=t \mid \mathbf X)} \right] \\ =& E\left[ \frac{E\left(Y^{(t)} \mid T = t, \mathbf X \right)\Pr(T = t\mid \mathbf X)}{\Pr(T=t \mid \mathbf X)} \right] \\ =& E\left[ E\left(Y^{(t)} \mid T = t, \mathbf X \right) \right] \\ =& E\left[ E\left(Y^{(t)} \mid \mathbf X \right) \right] \text{ (unconfoundedness)} \\ =& E\left[ Y^{(t)} \right]. \end{aligned} \]
To demonstrate that AIPW can be consistent even when propensity score is not correctly specified, we only need to focus on the general element \(E\left[\frac{1[T = t]Y}{\pi^{(t)}(\mathbf X)} - \frac{1[T=t] -\pi^{(t)}(\mathbf X)}{\pi^{(t)}(\mathbf X)} \mu_t(\mathbf X)\right]\).
When propensity score is wrong, i.e., \(\pi^{(t)}(\mathbf X)\neq \Pr(T = t\mid \mathbf X)\) but response surface estimation is correct, i.e., \(\mu_t(\mathbf X) = E(Y^{(t)} \mid \mathbf X)\), \[ \begin{aligned} & E\left[\frac{1[T = t]Y}{\pi^{(t)}(\mathbf X)} - \frac{1[T=t]}{\pi^{(t)}(\mathbf X)} \mu_t(\mathbf X) + \mu_t(\mathbf X)\right] \\ =& E\left[E\left(\frac{1[T = t]Y}{\pi^{(t)}(\mathbf X)} - \frac{1[T=t]}{\pi^{(t)}(\mathbf X)} \mu_t(\mathbf X) + \mu_t(\mathbf X) \mid \mathbf X \right)\right] \\ =& E\left[ \frac{E\left(1[T = t](Y - \mu_t(\mathbf X)) \mid \mathbf X\right)}{\pi^{(t)}(\mathbf X)}\right] + E[E(Y^{(t)} \mid \mathbf X)] \\ =& E\left[ \frac{\sum_a E\left(1[T = t](Y - \mu_t(\mathbf X)) \mid T = a,\mathbf X\right)\Pr(T = a \mid \mathbf X)}{\pi^{(t)}(\mathbf X)}\right] + E\left[Y^{(t)}\right] \\ =& E\left[ \frac{E\left(Y - \mu_t(\mathbf X) \mid T = t,\mathbf X\right)\Pr(T = t \mid \mathbf X)}{\pi^{(t)}(\mathbf X)}\right] + E\left[Y^{(t)}\right] \\ =& E\left[ \frac{\Pr(T = t \mid \mathbf X)}{\pi^{(t)}(\mathbf X)}\underbrace{\left(E\left(Y^{(t)} \mid \mathbf X\right) - \mu_t(\mathbf X) \right)}_{=0} \right] + E\left[Y^{(t)}\right] \text{ (unconfoundedness)} \\ =& E\left[Y^{(t)}\right] . \end{aligned} \] Therefore, under this situation, AIPW in equation (3) becomes \(\tau^{AIPW}=E\left[Y^{(1)}\right] - E\left[Y^{(-1)}\right] = \tau\).