OptTrialDesign背后的想法

在最优（临床）试验设计中，我们提出了一种寻找最佳实验设计的新颖方法，既可以最大限度地提高财务收益（即预期净收入，ENR），又可以符合监管要求。我们必须在两者中权衡。因为从制药公角度出发，较短的研究期限导致更早的市场准入，这有助于在LOE（排他性损失）之前最大化利润。但另一方面，监管机构和卫生技术评估（HTA）机构希望看到更加有保证的临床结果，这通常需要更长的研究时间。这两者之间存在一定冲突。

在具有time-to-event endpoint的实验中，给定target number of events，临床试验设计仍未完全确定。通常有三个参数，样本量（\(N\)），研究持续时间（\(S\)）和招人速度（\(r_a\)）（或招人时间，如果假设uniform \(r_a\)，在此我们不考虑，也不考虑对于具有中期分析的试验，可以按照类似的想法进行扩展），并且这三者存在无限的组合，从而形成了无数满足条件的试验设计。实际上，\(r_a\)不能取任意数字，因为它受到疾病发病率，类型和场所能力的限制。假设研究人员能够提供大致的\(r_a\)，甚至是一个范围，试验设计的自由度就会从3减少到2，并且我们能够在\(2×2\)平面中展示可行的设计集（如下图所示）。值得注意的是，研究持续时间与样本量之间需要权衡取舍。较大的样本量有助于加快试验，反之亦然。

金融中的CAPM模型

我们休息一会儿，转向资本资产定价模型（CAPM）。CAPM因其在分析投资组合定价方面的贡献而赢得了1990 年诺贝尔经济学奖，并因其简单性和实用价值而闻名。

在CAPM中，资产或投资组合的预期收益(\(ER_i\))可以通过以下方式计算, \[ ER_i = R_f + \beta_i(ER_m - R_f) \] 其中\(R_f\)是无风险收益率（例如10年期国债收益率）; \(\beta_i\) 代表基于市场风险的个人风险; 以及\(ER_m - R_f\)是市场风险溢价。基本上，这意味着在理想情况下，资产的风险越高，预期的回报就越高。

换句话说，我们可以说为了找到最佳资产，我们实际上需要最大化以下目标函数 \[ \max_i R_f + \beta_i(ER_m - R_f) \text{ for } i \in \text{可行集} \] 那么，什么是可行集？我们知道预期收益会随着资产的预期风险而增加，但是由于边际效用递减，预期收益应该有上限（不能达到无穷大），以及预期风险有下限（不能达到0）。通常，人们认为可行的集合是下图中抛物线所包围的区域。该抛物线（蓝色曲线）称为有效边界，它表示在给定风险下最大（以及最小）的预期收益（注意预期风险和收益的上下限限制）。不在有效边界上资产/投资组合（蓝色圆圈点；请注意，由于有效边界是假设性的，在实践中可能会被违反）是无效区域，因为总是可以在有效边界上找到具有相同预期风险的另一个资产，但预期收益更高。

让我们以优化问题的形式重写问题 \[ \begin{aligned} \max_i & \quad R_f + \beta_i(ER_m - R_f) \\ \text{s.t.} & \quad i \in \text{Efficient Frontier} \end{aligned} \] 其中，目标函数\(R_f + \beta_i(ER_m-R_f)\)实际上是资本市场线（capital market line, 图中的黑色直线）。 因此，最佳解决方案是切点（绿点）。

回到 Optimal Trial Design

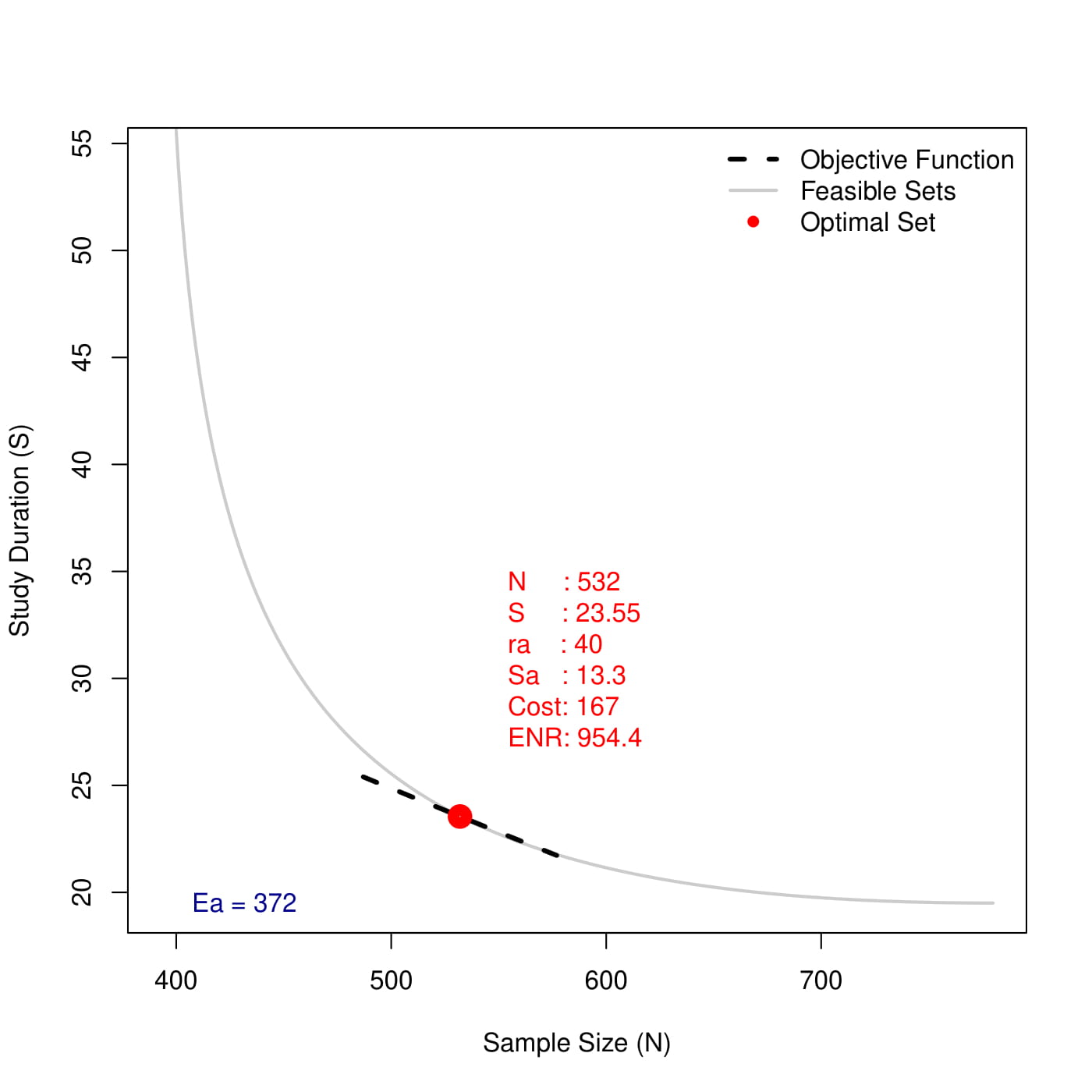
现在让我们回到最佳试验设计的问题上。 同样，我们要最大化ENR，可以表示为 \[ ENR = c_0(L-S) - c_1S - c_2N = c_0L - (c_0+c_1)S-c_2N \] 其中\(c_0(L-S)\)是预期销售额； \(L\)约是LOE的持续时间； \(c_1S\)是总维护成本； \(c_2N\)是总样本成本。 如上所述，可行集的“有效边界”是图1中的灰线。有效边界之上的其他可行集不是最佳的，因为我们总是可以在边界上找到较小的\(N\)或更小的\(S\)，使得ENR更高。

使用与CAPM完全相同的思想，可以将试设计问题转换为约束优化问题： \[ \begin{aligned} \max_i & \quad c_0L - (c_0+c_1)S_i-c_2N_i \\ \text{s.t.} & \quad i \in \text{有效边界} \end{aligned} \] 最优解也就是切点（红色点）。

（文章大致为Google机器翻译，请多多包涵。想详细了解内容，请参阅英文版。）